414. Уравнение
Дано целое
положительное число n. Сколько
решений в целых положительных числах имеет уравнение:
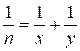
Вход. Целое число n
(1 ≤ n ≤ 109).
Выход. Количество
решений данного уравнения в натуральных числах.
|
Пример
входа |
Пример
выхода |
|
2 |
3 |
РЕШЕНИЕ
математика
Анализ алгоритма
Уравнение 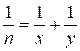 эквивалентно
эквивалентно  ,
, ![]() ,
,
![]()
Количество пар
решений (x, y) равно количеству представления числа n2 в виде произведения двух множителей. Оно в свою
очередь равно количеству делителей числа n2.
Если n = ![]() , то количество его делителей равно
, то количество его делителей равно
d(n) = (a1 + 1) * (a2
+ 1) * … * (ak + 1)
Ответом на
задачу будет значение d(n2)
= (2a1 + 1) * (2a2 + 1) * … * (2ak + 1).
Пример
Для n = 2 имеем: d(22) = 2 * 1 + 1 = 3.
Пусть n = 12. Поскольку 12 = 22 * 3
, то
d(122) = (2 * 2 + 1)
* (2 * 1 + 1) = 5 * 3 = 15
Число 122, например,
можно разложить на множители как 4 * 36. Решим ситему уравнений:
 ,
, 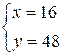
Одно из решений
исходного уравнения: ![]() .
.
Реализация алгоритма
Читаем входные
данные. Инициализируем текущий ответ задачи res единицей.
scanf("%d",&n); res = 1;
Для каждого простого делителя i числа n подсчитываем степень c,
с которой он входит в n. Умножаем
результат res на 2 * c + 1.
for(i = 2; i <= sqrt(n); i++)
{
c = 0;
while (n % i == 0)
{
n /= i; c++;
}
res = res * (2 * c
+ 1);
}
Если n > 1 по окончанию цикла, то оно равно простому делителю
исходного числа n. Этот делитель
входит в n со степенью 1,
следовательно res необходимо умножить
на 2 * 1 + 1 = 3.
if (n > 1) res *= 3;
Выводим результат.
printf("%d\n",res);
Java реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int res = 1, n = con.nextInt();
for(int i = 2; i <= Math.sqrt(n);
i++)
{
int c;
for(c = 0; n % i == 0; c++) n /= i;
res = res * (2 * c + 1);
}
if (n > 1) res *= 3;
System.out.println(res);
}
}
Python реализация
import math
n = int(input())
res = 1
for i in range(2, int(math.sqrt(n)) + 1):
c = 0;
while n % i == 0:
n = n // i
c += 1
res = res * (2 * c + 1)
if n > 1: res *= 3
print(res)